how to find asymptotes of a rational function
The Graph of a Rational Function, in many cases, have one or more Horizontal Lines, that is, as the values of x tends towards Positive or Negative Infinity, the Graph of the Function approaches these Horizontal lines, getting closer and closer but never touching or even intersecting these lines. These Lines are called Horizontal Asymptotes. This Article will show How to find these Horizontal lines, by looking at some Examples.
Given the Rational Function, f(x) = 1/(x-2), we can immediately see that when x=2, we have a Vertical Asymptote, ( To know about Vertical Asympyotes, please go to the Article, "How to Find the Difference between the Vertical Asymptote of...", by this same Author, Z-MATH ).
The Horizontal Asymptote of the Rational Function, f(x) = 1/(x-2), can be found by doing the following: Divide both the Numerator ( 1 ), and the Denominator (x-2), by the highest degreed term in the Rational Function, which in this case, is the Term 'x'.
So, f(x)= (1/x)/[(x-2)/x]. That is, f(x) = (1/x)/[(x/x)-(2/x)], where (x/x)=1. Now we can express the Function as, f(x) = (1/x)/[1-(2/x)], As x approaches infinity, both the terms (1/x) and (2/x) approaches Zero, (0). Let us say, " The Limit of (1/x) and (2/x) as x approaches infinity, is equal to Zero (0) ".
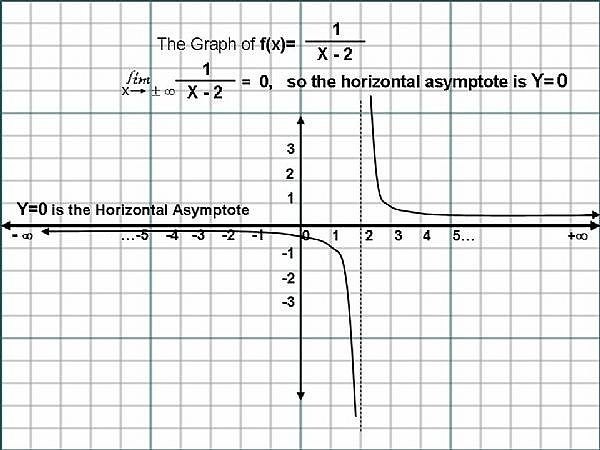
The Horizontal line y = f(x)= 0/(1-0) = 0/1 = 0, that is, y=0, is the Equation of the Horizontal Asymptote. Please Click on the Image for a better understanding.
Given the Rational Function, f(x)= x/(x-2), to find the Horizontal Asymptote, we Divide both the Numerator ( x ), and the Denominator (x-2), by the highest degreed term in the Rational Function, which in this case, is the Term 'x'.
So, f(x)= (x/x)/[(x-2)/x]. That is, f(x) = (x/x)/[(x/x)-(2/x)], where (x/x)=1. Now we can express the Function as, f(x) = 1/[1-(2/x)], As x approaches infinity, the term (2/x) approaches Zero, (0). Let us say, " The Limit of (2/x) as x approaches infinity, is equal to Zero (0) ".
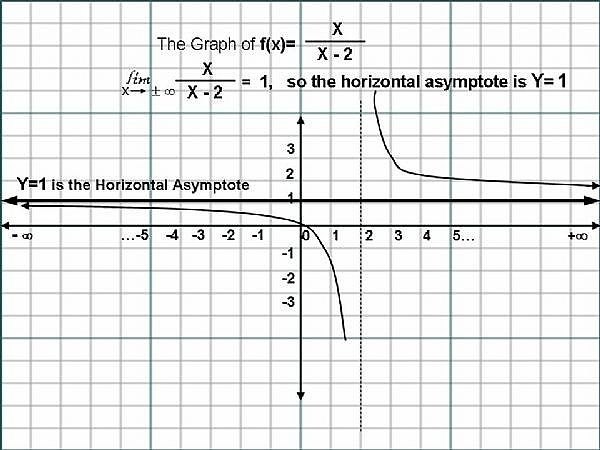
The Horizontal line y = f(x)= 1/(1-0) = 1/1 = 1, that is, y=1, is the Equation of the Horizontal Asymptote. Please Click on the Image for a better understanding.
In summary, given a Rational Function f(x)= g(x)/h(x),where h(x) ≠ 0, if the degree of g(x) is less than the degree of h(x), then the Equation of the Horizontal Asymptote is y=0. If the degree of g(x) is equal to the degree of h(x), then the Equation of the Horizontal Asymptote is y=( to the ratio of the leading coefficients ). If the degree of g(x) is greater than the degree of h(x),then there is no Horizontal Asymptote.
For Examples; If f(x) = (3x^2 + 5x - 3)/(x^4 -5), the Equation of the Horizontal Asymptote is..., y=0, since the degree of the Numerator function is 2, which is less than 4, 4 being the degree of the Denominator Function.
If f(x) = (5x^2 - 3)/(4x^2 +1), the Equation of the Horizontal Asymptote is..., y=(5/4), since the degree of the Numerator function is 2, which is equal to the same degree as the Denominator Function.
If f(x) =(x^3 +5)/(2x -3), there is NO Horizontal Asymptote, since the degree of the Numerator Function is 3, which is greater than 1, 1 being the degree of the Denominator Function.
Things You'll Need
- Paper and
- Pencil
how to find asymptotes of a rational function
Source: https://sciencing.com/of-graph-of-rational-function-4696630.html
Posted by: lemoshatill1975.blogspot.com

0 Response to "how to find asymptotes of a rational function"
Post a Comment